Binary Search Tree:
A Binary Search Tree is a Binary Tree data structure (a tree in which each node has at most two children) which has the following properties:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
- There must be no duplicate nodes.
Traversal of binary search tree refers to the process of visiting each node one-by-one. For binary tree, we generally use the following 3 types of traversal:
- Pre-Order
- Visit the root.
- Traverse the left subtree.
- Traverse the right subtree.
- In-Order
- Traverse the left subtree.
- Visit the root.
- Traverse the right subtree.
- Post-Order
- Traverse the left subtree.
- Traverse the right subtree.
- Visit the root.
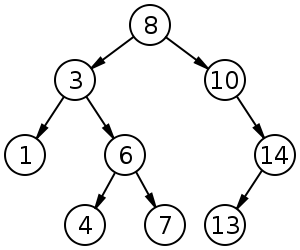
For this tree, the Preorder traversal will be:
8, 3, 1, 6, 4, 7, 10, 14, 13
And the Inorder traversal will be:
1, 3, 4, 6, 7, 8, 10, 13, 14
And the Postorder traversal will be:
1, 4, 7, 6, 3, 13, 14, 10, 8
Here note that the Inorder traversal of a Binary Search tree results in an ascending order list.
Checkout Program to check if a Tree is a Binary Search Tree.
Program to implement Binary Search Tree in C++:
# include <iostream>
# include <cstdlib>
using namespace std;
// Binary Search Tree Node Declaration
struct node
{
int info;
struct node *left;
struct node *right;
}*root;
// Class Declaration for Binary Search Tree
class BST
{
public:
void find(int, node **, node **);
void insert(node *,node *) ;
void del(int);
void case_a(node *,node *);
void case_b(node *,node *);
void case_c(node *,node *);
void preorder(node *);
void inorder(node *);
void postorder(node *);
void display(node *, int);
BST()
{
root = NULL;
}
};
// Main Contains Menu
int main()
{
int choice, num;
BST bst;
node *temp;
while (1)
{
// Main menu for Binary Search Tree Operations
cout<<"-----------------"<<endl;
cout<<"Operations on BST"<<endl;
cout<<"-----------------"<<endl;
cout<<"1.Insert Element "<<endl;
cout<<"2.Delete Element "<<endl;
cout<<"3.Inorder Traversal"<<endl;
cout<<"4.Preorder Traversal"<<endl;
cout<<"5.Postorder Traversal"<<endl;
cout<<"6.Display"<<endl;
cout<<"7.Quit"<<endl;
cout<<"Enter your choice : ";
cin>>choice;
switch(choice)
{
case 1:
temp = new node;
cout<<"Enter the number to be inserted : ";
cin>>temp->info;
bst.insert(root, temp);
case 2:
if (root == NULL)
{
cout<<"Tree is empty, nothing to delete"<<endl;
continue;
}
cout<<"Enter the number to be deleted : ";
cin>>num;
bst.del(num);
break;
case 3:
cout<<"Inorder Traversal of BST:"<<endl;
bst.inorder(root);
cout<<endl;
break;
case 4:
cout<<"Preorder Traversal of BST:"<<endl;
bst.preorder(root);
cout<<endl;
break;
case 5:
cout<<"Postorder Traversal of BST:"<<endl;
bst.postorder(root);
cout<<endl;
break;
case 6:
cout<<"Display BST:"<<endl;
bst.display(root,1);
cout<<endl;
break;
case 7:
exit(1);
default:
cout<<"Wrong choice"<<endl;
}
}
}
// Find Element in the Binary Search Tree
void BST::find(int item, node **par, node **loc)
{
node *ptr, *ptrsave;
if (root == NULL)
{
*loc = NULL;
*par = NULL;
return;
}
if (item == root->info)
{
*loc = root;
*par = NULL;
return;
}
if (item < root->info)
ptr = root->left;
else
ptr = root->right;
ptrsave = root;
while (ptr != NULL)
{
if (item == ptr->info)
{
*loc = ptr;
*par = ptrsave;
return;
}
ptrsave = ptr;
if (item < ptr->info)
ptr = ptr->left;
else
ptr = ptr->right;
}
*loc = NULL;
*par = ptrsave;
}
// Inserting Element into the Binary Search Tree
void BST::insert(node *tree, node *newnode)
{
if (root == NULL)
{
root = new node;
root->info = newnode->info;
root->left = NULL;
root->right = NULL;
cout<<"Root Node is Added"<<endl;
return;
}
if (tree->info == newnode->info)
{
cout<<"Element already in the tree"<<endl;
return;
}
if (tree->info > newnode->info)
{
if (tree->left != NULL)
{
insert(tree->left, newnode);
}
else
{
tree->left = newnode;
(tree->left)->left = NULL;
(tree->left)->right = NULL;
cout<<"Node Added To Left"<<endl;
return;
}
}
else
{
if (tree->right != NULL)
{
insert(tree->right, newnode);
}
else
{
tree->right = newnode;
(tree->right)->left = NULL;
(tree->right)->right = NULL;
cout<<"Node Added To Right"<<endl;
return;
}
}
}
// Delete Element from the Binary Search tree
void BST::del(int item)
{
node *parent, *location;
if (root == NULL)
{
cout<<"Tree empty"<<endl;
return;
}
find(item, &parent, &location);
if (location == NULL)
{
cout<<"Item not present in tree"<<endl;
return;
}
if (location->left == NULL && location->right == NULL)
case_a(parent, location);
if (location->left != NULL && location->right == NULL)
case_b(parent, location);
if (location->left == NULL && location->right != NULL)
case_b(parent, location);
if (location->left != NULL && location->right != NULL)
case_c(parent, location);
free(location);
}
// * Case A
void BST::case_a(node *par, node *loc )
{
if (par == NULL)
{
root = NULL;
}
else
{
if (loc == par->left)
par->left = NULL;
else
par->right = NULL;
}
}
// * Case B
void BST::case_b(node *par, node *loc)
{
node *child;
if (loc->left != NULL)
child = loc->left;
else
child = loc->right;
if (par == NULL)
{
root = child;
}
else
{
if (loc == par->left)
par->left = child;
else
par->right = child;
}
}
// * Case C
void BST::case_c(node *par, node *loc)
{
node *ptr, *ptrsave, *suc, *parsuc;
ptrsave = loc;
ptr = loc->right;
while (ptr->left != NULL)
{
ptrsave = ptr;
ptr = ptr->left;
}
suc = ptr;
parsuc = ptrsave;
if (suc->left == NULL && suc->right == NULL)
case_a(parsuc, suc);
else
case_b(parsuc, suc);
if (par == NULL)
{
root = suc;
}
else
{
if (loc == par->left)
par->left = suc;
else
par->right = suc;
}
suc->left = loc->left;
suc->right = loc->right;
}
// Pre Order Traversal
void BST::preorder(node *ptr)
{
if (root == NULL)
{
cout<<"Tree is empty"<<endl;
return;
}
if (ptr != NULL)
{
cout<<ptr->info<<" ";
preorder(ptr->left);
preorder(ptr->right);
}
}
// In Order Traversal
void BST::inorder(node *ptr)
{
if (root == NULL)
{
cout<<"Tree is empty"<<endl;
return;
}
if (ptr != NULL)
{
inorder(ptr->left);
cout<<ptr->info<<" ";
inorder(ptr->right);
}
}
// Postorder Traversal
void BST::postorder(node *ptr)
{
if (root == NULL)
{
cout<<"Tree is empty"<<endl;
return;
}
if (ptr != NULL)
{
postorder(ptr->left);
postorder(ptr->right);
cout<<ptr->info<<" ";
}
}
// Display Binary Search Tree Structure
void BST::display(node *ptr, int level)
{
int i;
if (ptr != NULL)
{
display(ptr->right, level+1);
cout<<endl;
if (ptr == root)
cout<<"Root->: ";
else
{
for (i = 0;i < level;i++)
cout<<" ";
}
cout<<ptr->info;
display(ptr->left, level+1);
}
}
OUTPUT:
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 1
Enter the number to be inserted : 8
Root Node is Added
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
Root->: 8
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 1
Enter the number to be inserted : 9
Node Added To Right
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
9
Root->: 8
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 1
Enter the number to be inserted : 5
Node Added To Left
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
9
Root->: 8
5
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 1
Enter the number to be inserted : 11
Node Added To Right
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
11
9
Root->: 8
5
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 1
Enter the number to be inserted : 3
Node Added To Left
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 1
Enter the number to be inserted : 7
Node Added To Right
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
11
9
Root->: 8
7
5
3
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 1
Enter the number to be inserted : 10
Node Added To Left
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
11
10
9
Root->: 8
7
5
3
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 2
Enter the number to be deleted : 10
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
11
9
Root->: 8
7
5
3
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 3
Inorder Traversal of BST:
3 5 7 8 9 11
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 4
Preorder Traversal of BST:
8 5 3 7 9 11
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 5
Postorder Traversal of BST:
3 7 5 11 9 8
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 2
Enter the number to be deleted : 8
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
11
Root->: 9
7
5
3
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 1
Enter the number to be inserted : 10
Node Added To Left
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
11
10
Root->: 9
7
5
3
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 1
Enter the number to be inserted : 15
Node Added To Right
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
15
11
10
Root->: 9
7
5
3
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 4
Preorder Traversal of BST:
9 5 3 7 11 10 15
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 5
Postorder Traversal of BST:
3 7 5 10 15 11 9
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 6
Display BST:
15
11
10
Root->: 9
7
5
3
-----------------
Operations on BST
-----------------
1.Insert Element
2.Delete Element
3.Inorder Traversal
4.Preorder Traversal
5.Postorder Traversal
6.Display
7.Quit
Enter your choice : 7
------------------
(program exited with code: 1)
Press return to continue